自从生物物理学家Hopfield^[1]在20世纪80年代首次提出人工神经网络以来，人工神经网络得到了广泛的研究。如今，人工神经网络在联想记忆、图像处理、优化组合等方面得到了广泛的应用^[2,3,4,5]。在这些领域对人工神经网络系统的稳定性进行研究是十分必要的^[6,7,8]。

近年来，随着数域的扩张，人工神经网络主要有实数神经网络、复数神经网络以及四元数神经网络。四元数由一个实部和3个虚部构成，四元数对数据信息的存储能力比实数和复数都要强。一个四元数的数据存储能力是一个实数的4倍，是一个复数的2倍。因此，四元数神经网络在处理高维数据时比实数神经网络以及复数神经网络都更有优势。例如，在与图像有关的应用中，一种颜色往往由红色（R）、绿色（G）和蓝色（B）3种基本颜色按照各自的像素值合成，将 R、G、B 值分别对应于纯四元数的3个虚部部分i、j和k的系数时，一种颜色便可以用一个纯虚数唯一表示，一张图片可以用一个纯四元数矩阵唯一表示^[9,10]。

然而，之前研究的四元数神经网络涉及的四元数是定义在哈密顿（Hamilton）乘法规则之下的，此规则不满足乘法交换律。为了解决这个问题，本文给出了满足乘法交换律的四元数（以下简称交换四元数），它保留了四元数相对于实数及复数的基本优势，即具有更好的数据存储能力。但在新的乘法规则下，对交换四元数神经网络（commutative quaternion valued neural network，CQVNN）的研究也面临着许多挑战，例如：交换四元数同时存在 3个共轭，交换四元数的模表示十分复杂，交换四元数不满足三角不等式等。这些局限使得那些适用于实数、复数以及不可交换四元数的不等式理论不适用于交换四元数。为了解决这些问题，本文通过交换四元数的乘法规则将CQVNN转化为实数神经网络，进而研究其稳定性。

本文的结构组织如下：第2节介绍交换四元数以及交换四元数神经网络，给出一些引理及定义；第3节给出交换四元数神经网络渐近稳定的充分条件；第4节用一个数值案例验证了得到的结论的有效性；第5节对本文进行总结。

一个交换四元数可以表示为：

其中，q^R、q^I、q^J、$q^K\in ℝ$分别表示交换四元数的第一部分、第二部分、第三部分以及第四部分的数值，虚单位i、j、k满足如下运算规则。

交换四元数q存在如下3种共轭：

q的模定义如下：

对于另一个交换四元数 $p=p^R+p^{I}i+p^{J}j+p^{K}k$来说，p与q的乘积定义如下：

注 1 此规则定义的四元数乘法虽然满足了乘法交换律，但由此衍生出来的交换四元数的模不满足三角不等式。例如：

而$\left|\right|q_1+q_2\left|\right|=1>\left|\right|q_1\left|\right|+\left|\right|q_2\left|\right|=0$。因此，交换四元数不能直接使用以往的许多不等式，为了克服这一困难，下面的四元数神经网络将被等价转化为实数神经网络进行研究。

考虑如下的四元数神经网络：

其中，$\text{q}(t)={\left(q_1(t),q_2(t),\cdots ,q_n(t)\right)}^{\text{T}}\in {\mathbb{Q}}^n$是具有n个神经元的 CQVNN 在 t 时刻的状态向量。$C=\text{diag}\{c_1,c_{\text{2}},\cdots ,c_n\}\in {ℝ}^n$,$c_i>0(i=1,2,\cdots ,n)$，是自反馈连接矩阵，$A=A^R+A^{I}i+A^{J}j+A^{K}k\in {\mathbb{Q}}^{n\times n}$是连接权矩阵，$B=B^R+B^{I}i+B^{J}j+B^{K}k\in {\mathbb{Q}}^{n\times n}$是时滞连接权矩阵。$f(q(t))={\left(f_1(q_1(t)),f_2(q_2(t)),\cdots ,f_n(q_n(t))\right)}^{\text{T}}\in {\mathbb{Q}}^n$是交换四元数值的激活函数， $g(q(t-\tau (t)))={\left(g_1(q_1(t-\tau (t))),g_2(q_2(t-\tau (t))),\cdots g_n(q_n(t-\tau (t)))\right)}^{\text{T}}\in {\mathbb{Q}}^n$是带有时滞的交换四元数值的激活函数。$u=u^R+u^{I}i+u^{J}j+u^{K}k={\left(u_1,u_2,\cdots ,u_n\right)}^{\text{T}}\in {\mathbb{Q}}^n$是外部输入向量，$0\le \tau (t)\le \tau (\tau >0)$是时滞项。式（3）的初始条件如下：

其中，t₀为式（3）表示的系统的初始时间，τ为时滞项τ(t)的上界，$\phi (s)$为系统初始条件。

假设1 设$q(t)=q^R(t)+q^I(t)i+q^J(t)j+q^K(t)k$,q^R(t)、q^I(t)、q^J(t)、$q^K(t)\in ℝ$。对于所有的$m(m=1,2,\cdots ,n)$ ，f_m(q(t))和g_m(q(t-τ(t)))能够表示成：

其中，$f_m^{\mathcal{l}}(·)$,$g_m^{\mathcal{l}}(·):{ℝ}^n\to {ℝ}^n$,$\mathcal{l}\in \{R,I,J,K\}$，满足：

其中，l_m、${\tilde{l}}_m$是利普希茨（Lipschitz）常数，记：

基于式（2）和假设 1，式（3）可以被重写成如下形式：

根据式（4）～式（7），可以得到：

其中，

通过假设1，可以得到：

其中，$L\text{=diag{}{L}^R,L^I,L^J,L^K\text{}}$,$\tilde{L}\text{=diag{}{\tilde{L}}^R,{\tilde{L}}^I,{\tilde{L}}^J,{\tilde{L}}^K\text{}}$。

定义 1 若常数向量$\tilde{q}={\left({\tilde{q}}_1,{\tilde{q}}_2,\cdots ,{\tilde{q}}_n\right)}^T$满足$-C\tilde{q}+Af(\tilde{q})+Bg(\tilde{q})+u=0$，则称常数向量$\tilde{q}$是交换四元数神经网络（式（3））的平衡点。

为了保证式（7）表示的系统有唯一平衡点，需要做如下假设。

假设2 $\widehat{C}-\left|\widehat{A}\right|L-\left|\widehat{B}\right|\tilde{L}$ 是一个非奇异M矩阵。

假设 3 设$K=\widehat{C}-\left|\widehat{A}\right|L-\left|\widehat{B}\right|\tilde{L}$ ，$K\text{+}{K}^{\text{T}}$是一个非奇异矩阵。

定理1 如果假设1、假设2成立，则式（8）表示的系统存在唯一的平衡点。

定理2 如果假设1、假设3成立，则式（8）表示的系统存在唯一的平衡点。

证明 通过文献[11]中的定理1与定理2，可以直接得到本文的定理1和定理2。

为了更加方便地研究式（8）表示的实数系统，将其系统平衡点平移至原点。假设$\tilde{Q}={\left({\left({\tilde{q}}^R\right)}^T,\left({\tilde{q}}^I\right),{\left({\tilde{q}}^J\right)}^T{\left({\tilde{q}}^J\right)}^T\right)}^T$,是式（8）表示的系统的平衡点，做变换$\overline{Q}(t)=Q(t)-\tilde{Q}$，则式（8）变为下面的向量形式：

其中，$F(\overline{Q}(t))\text{=}\widehat{F}(\overline{Q}(t)+\tilde{Q})-\widehat{F}(\tilde{Q})$ ,$G(\overline{Q}(t-\tau (t)))=\widehat{G}(\overline{Q}(t-\tau (t))+\tilde{Q})-\widehat{G}(\tilde{Q})$。

显然，式（9）表示的实值系统原点的稳定性与式（8）表示的实值系统及交换四元数神经网络（如式（3）所示）的平衡点的稳定性是等价的。

下面对式（9）的渐近稳定性做一个系统的定义。

定义2 若对于任意给定的ε>0，都能找到正数$\delta =\delta (\epsilon ,t_0)$，使得当$\left|\right|x_0\left|\right|<\delta$|和t>t₀时，式（9）的解$\overline{Q}(t)=\overline{Q}(t,t_0,x_0)$ 满足 $\left|\right|\overline{Q}(t,t_0,x_0)\left|\right|<\epsilon$，则称式（9）的零解是稳定的。

定义 3 设U是$\left|\right|\overline{Q}(t,t_0,x_0)\left|\right|<\epsilon$中包含坐标原点的一个开区域，若对于所有的x₀∈U和任意给定的ε>0，都能找到正数$T=T(\epsilon ,t_0,x_0)$，使得当t>t₀+T时，式（9）的解$\overline{Q}(t)=\overline{Q}(t,t_0,x_0)$满足$\left|\right|\overline{Q}(t,t_0,x_0)\left|\right|<\epsilon$| ，则称式（9）的零解是吸引的，称U是式（9）的零解的一个吸引域。

定义4 若式（9）的零解既是稳定的又是吸引的，则称式（9）的零解是渐近稳定的；若式（9）的零解的吸引域是整个${ℝ}^n$，则称式（9）的零解是全局渐近稳定的。

注2 经过变换后，式（9）的平衡点平移至原点，此时称系统的解为零解。利用极限的形式可以给出式（9）的零解稳定和吸引的直观描述为：

当对于一切t>t₀，$\underset{x_0\to 0}{\lim }x(t,t_0,x_0)=0$时，称式（9）的零解是稳定的；

当对于一切的x₀∈U，$\underset{t\to \infty }{\lim }x(t,t_0,x_0)=0$时，称式（9）的零解是吸引的。

引理1 对于任意$a,b\in {ℝ}^n$，如果$P$是一个正定的对称矩阵，则：

证明 根据文献[12]中的引理2，可以直接得到这个结果。

引理2^[12]当且仅当下面的两个式子之一成立：

则有实对称矩阵：

其中，$S_{11}^{\text{T}}=S_{11}$、$S_{\text{12}}^{\text{T}}=S_{\text{21}}$和$S_{\text{22}}^{\text{T}}=S_{\text{22}}$。

引理3^[13]若在原点的领域U内，存在正定（负定）函数V(t)使得$\dot{V}(t)$是负定（正定）的，那么式（9）的零解是渐近稳定的。

注 3 无论是在深度学习领域还是在神经网络动力学行为研究领域，考虑比较多的都是实数神经网络或者复数值神经网络，这些神经网络在处理三维或者四维等高维数据时具有一定的局限性。于是，近几年出现了基于Hamilton规则的四元数神经网络，这种神经网络对高维数据的处理具有一定的优势。但是，基于Hamilton规则的四元数不满足乘法交换律，本文给出了可交换的四元数神经网络模型，一定程度上解决了基于Hamilton规则的四元数神经网络具有的局限性。

本节将基于李雅普诺夫（Lyapunov）稳定性理论给出式（8）表示的系统的唯一平衡点渐近稳定的充分性判据。

定理3 在假设1、2的条件下，如果存在4个正定对角矩阵$P_{\text{1}}$、$P_2$、${\Gamma }_1$、${\Gamma }_2$使得如下线性矩阵不等式（linear matrix inequality，LMI）条件成立：

则式（9）表示系统的唯一平衡点是渐近稳定的。

证明：构造如下Lyapunov函数：

根据假设1及引理1计算V()t 的导数：

根据引理 2 和式（10）得出$-\widehat{C}{P}_1-P_1\widehat{C}+P_2+P_1\widehat{A}{\Gamma }_1^{-1}{\widehat{A}}^{\text{T}}P+P_1\widehat{B}{\Gamma }_1^{-1}{\widehat{B}}^{\text{T}}P<0$，结合式（11），得到V(t)<0。又因为V(t)是径向无界的，根据一般的Lyapunov 稳定性理论（引理 3）得知式（9）表示的系统的唯一平衡点是渐近稳定的。

为了验证定理3得到的稳定性判据的有效性，本节将选择一个符合定理 3 的系统案例，并通过Matlab绘制其解曲线并观察解的轨迹，进而判定本文所得结果的有效性。另外，考虑到现实中噪声的影响，在案例2中对系统的连接权以及系统的外部输入项添加一个正态分布的（0,1）噪声，然后观察分析系统解曲线的性态。

（1）案例1

考虑如下二维交换四元数神经网络：

其中，$A={\left(a_{ij}\right)}_{2\times 2}$,$B={\left(b_{ij}\right)}_{2\times 2}$,

取$L^{\mathcal{l}}={\tilde{L}}^{\mathcal{l}}=\text{diag}\{1,1\}$,$\mathcal{l}\in \{R,I,J,K\}$ ，容易验证$\widehat{C}-\left|\widehat{A}\right|L-\left|\widehat{B}\right|\tilde{L}$是L矩阵，经计算得到$\widehat{C}-\left|\widehat{A}\right|L-\left|\widehat{B}\right|\tilde{L}$的特征值为 0.694、4.669、4.000、3.900、3.806、3.400、3.432、3.300，它们全具有正实部，则$\widehat{C}-\left|\widehat{A}\right|L-\left|\widehat{B}\right|\tilde{L}$是非奇异M矩阵。通过Matlab中的 YALMIP 工具包，得到正定的对角矩阵$P_1$、$P_2$、${\Gamma }_1$、${\Gamma }_2$，它们满足式（10）和式（11）。

通过定理 3，可以得到式（12）表示的系统是渐近稳定的。这里选取系统的初始值为：

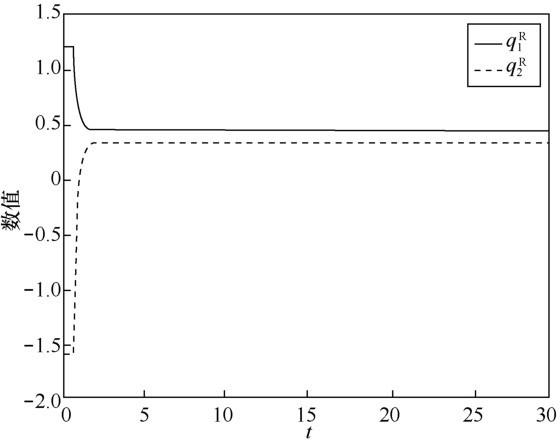
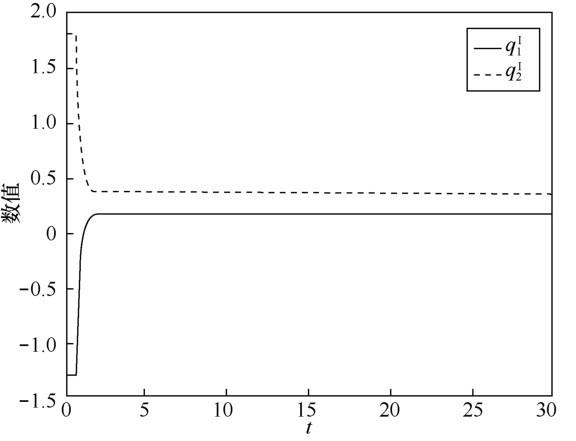
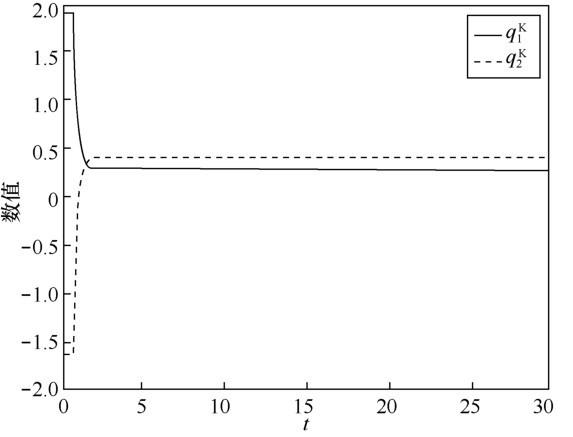
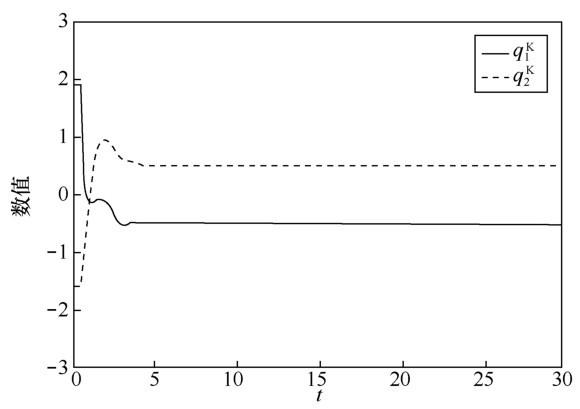
其中，s∈[-0.5,0]，图1,图2,图3,图4展示了所给系统的4 个部分的状态轨迹，这里的状态轨迹是指系统的解曲线，从这4幅图中可以看到每个神经元都收敛到稳定状 态，收敛 点为 $\tilde{q}={\left({\tilde{q}}_{ij}\right)}_{2\times 1}$，其中${\tilde{q}}_{11}=0.439+0.186i+0.383j+0.287k$，${\tilde{q}}_{21}=0.324+0.362i+0.274j+0.386k$。

图1,图2,图3,图4,图5,图6,图7,图8q₁和q₂分别为式（12）所示系统的第一维和第二维的解，t表示q₁和q₂的自变量。

（2）案例2

对案例1中涉及的系统的连接权参数$A$和$B$以及外部输入$u$添加一个正态分布的（0,1）噪声，通过Matlab的数值仿真结果如图5～图8所示，结果显示每一个神经元都收敛于平衡点。可见系统在受到一定噪声干扰时，其稳定性不会受到影响。

注 4 按照数据类型，可将神经网络分为实值神经网络、复值神经网络和四元数神经网络。实值神经网络的应用十分广泛，但是它无法高效地处理诸如二维仿射变换或者三维仿射变换等几何变换问题。为了解决这一问题，学者们发现复值神经网络能够将二维空间中的一个点数据建模成一个单独的整体，而不是两个数据单元的集合，这就使得复值神经网络在处理二维数据的仿射变换时，比实值神经网络更为高效快捷。然而，在实际生活中，常常需要处理三维数据，例如，与图像有关的应用、方向预测以及机器人操控等。近年来，学者们发现采用四元数可以直接对高维数据进行编码处理，大幅提升了处理效率，尤其在处理三维空间变换时非常高效简洁。目前四元数神经网络已经在卫星的姿态控制、彩色图像压缩、计算机图像学、彩色微光夜视以及机器人运动控制等诸多领域展现了良好的应用前景^{[14,15,16,17]}。因此，关于四元数神经网络稳定性的研究是十分有意义的。然而，目前研究的四元数神经网络不满足乘法交换律，即存在一定的局限性。本文提出的可交换四元数神经网络在一定程度上解决了这一局限性。目前，关于本文所涉及的交换四元数神经网络的渐近稳定性研究较少，因此本文研究具有一定的创新性。

本文对交换四元数神经网络的渐近稳定性进行了研究。首先介绍了交换四元数的一些基本概念及运算，然后提出了交换四元数的神经网络。考虑到交换四元数具有3个共轭这一事实所带来的各种问题，文中将交换四元数神经网络分解成4个实值神经网络，通过不等式理论、Lyapunov稳定性理论以及拓扑度理论，得到了一些交换四元数神经网络平衡点存在且唯一的充分条件以及平衡点渐近稳定的LMI条件。最后，提供了两个案例来证明所提出的LMI条件的有效性。